QWZ模型简介
QWZ(Qi-Wu-Zhang)模型是研究拓扑绝缘体最简单且最基本的模型之一,由Qi、Wu和Zhang三位物理学家提出。这个模型描述了二维晶格上的电子跃迁系统,可以展示拓扑相变和拓扑不变量(如陈数)的特性。
本文将介绍QWZ模型的基本原理、能带结构、Berry曲率以及陈数计算,并展示相关的数值模拟结果。
理论基础
QWZ模型的哈密顿量可以表示为:
$$H(\mathbf{k}) = \begin{pmatrix} 2u(\cos k_x + \cos k_y) & t(\sin k_x - i\sin k_y) \ t(\sin k_x + i\sin k_y) & -2u(\cos k_x + \cos k_y) \end{pmatrix}$$
其中:
- $u$ 是质量项参数
- $t$ 是跃迁强度参数
- $k_x$ 和 $k_y$ 是动量空间中的波矢
该哈密顿量可以重写为与泡利矩阵相关的形式:
$$H(\mathbf{k}) = d_x(\mathbf{k})\sigma_x + d_y(\mathbf{k})\sigma_y + d_z(\mathbf{k})\sigma_z$$
其中 $\sigma_i$ 是泡利矩阵,而:
- $d_x(\mathbf{k}) = t\sin k_x$
- $d_y(\mathbf{k}) = t\sin k_y$
- $d_z(\mathbf{k}) = 2u(\cos k_x + \cos k_y)$
能带结构
QWZ模型的能带结构对于理解其拓扑性质至关重要。下图展示了在标准参数设置($u=1.0$,$t=1.0$)下的能带:
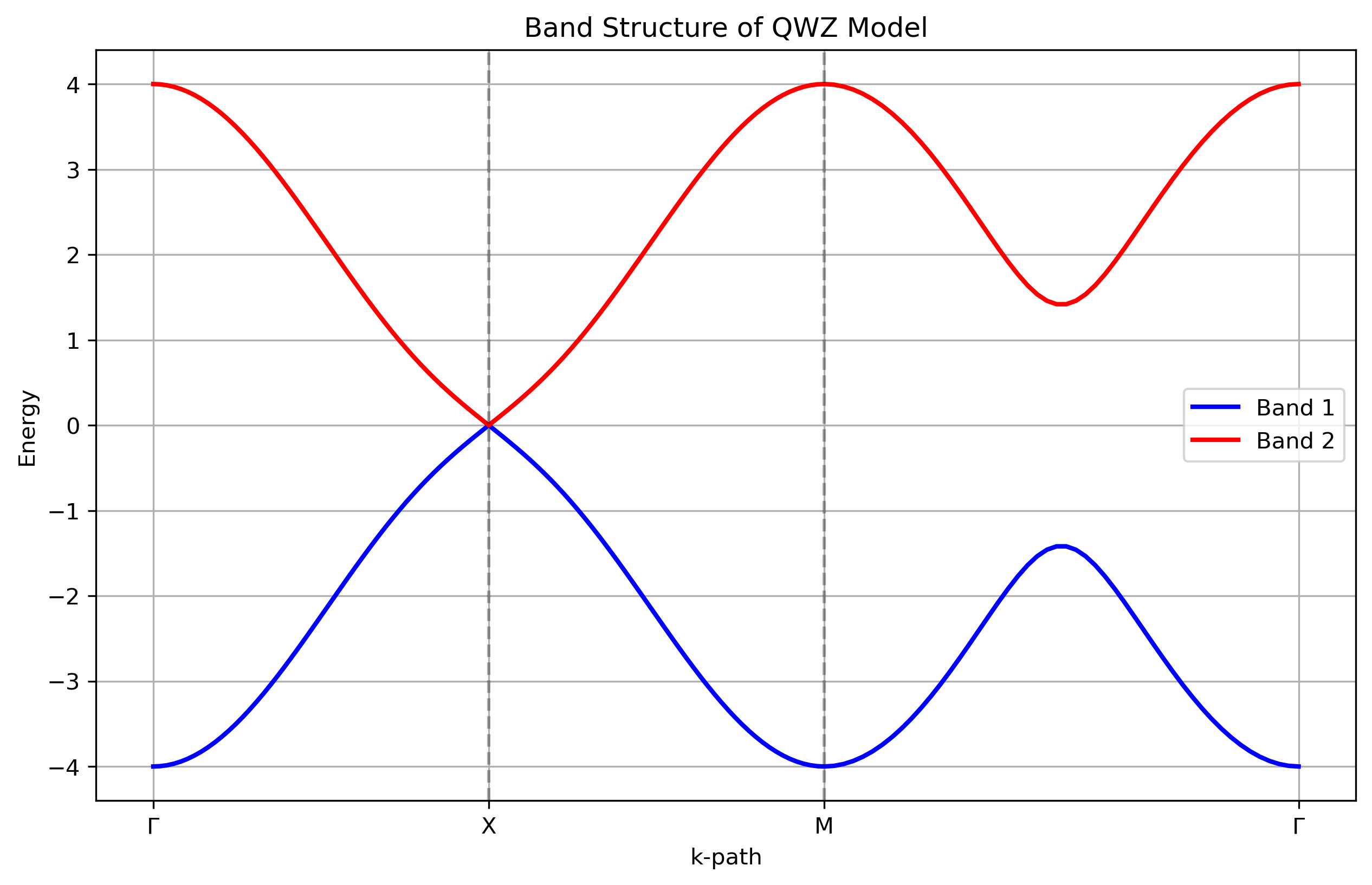
从能带图中可以看出,在布里渊区的高对称点处,能隙会发生变化。特别是当 $u$ 参数改变时,系统可能会经历从拓扑平庸态到拓扑非平庸态的相变。
Berry曲率与陈数
Berry曲率是拓扑绝缘体中表征拓扑性质的重要量。在QWZ模型中,Berry曲率可以通过计算本征态在动量空间中的导数来获得。
二维Berry曲率的分布:
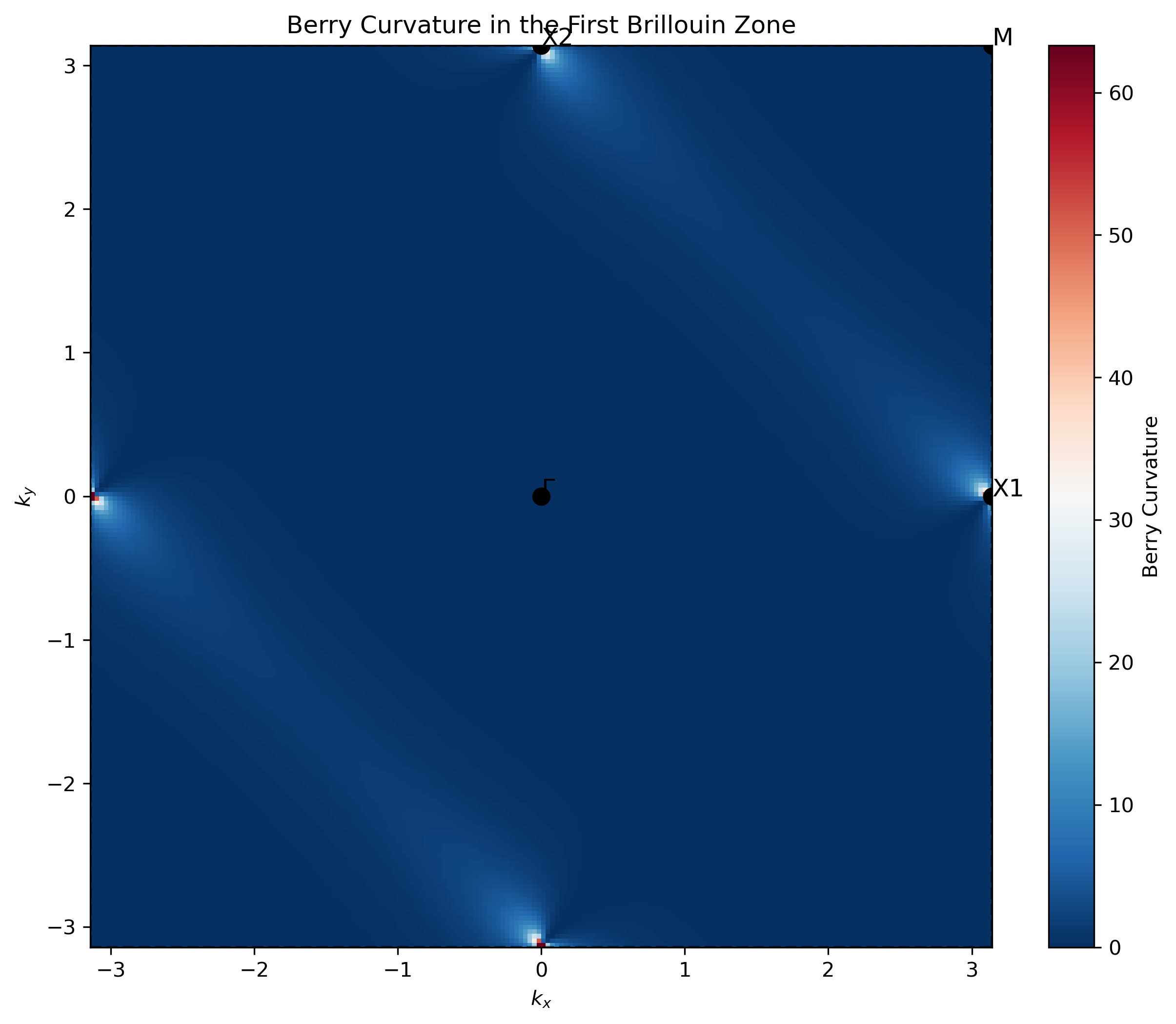
三维Berry曲率可视化:
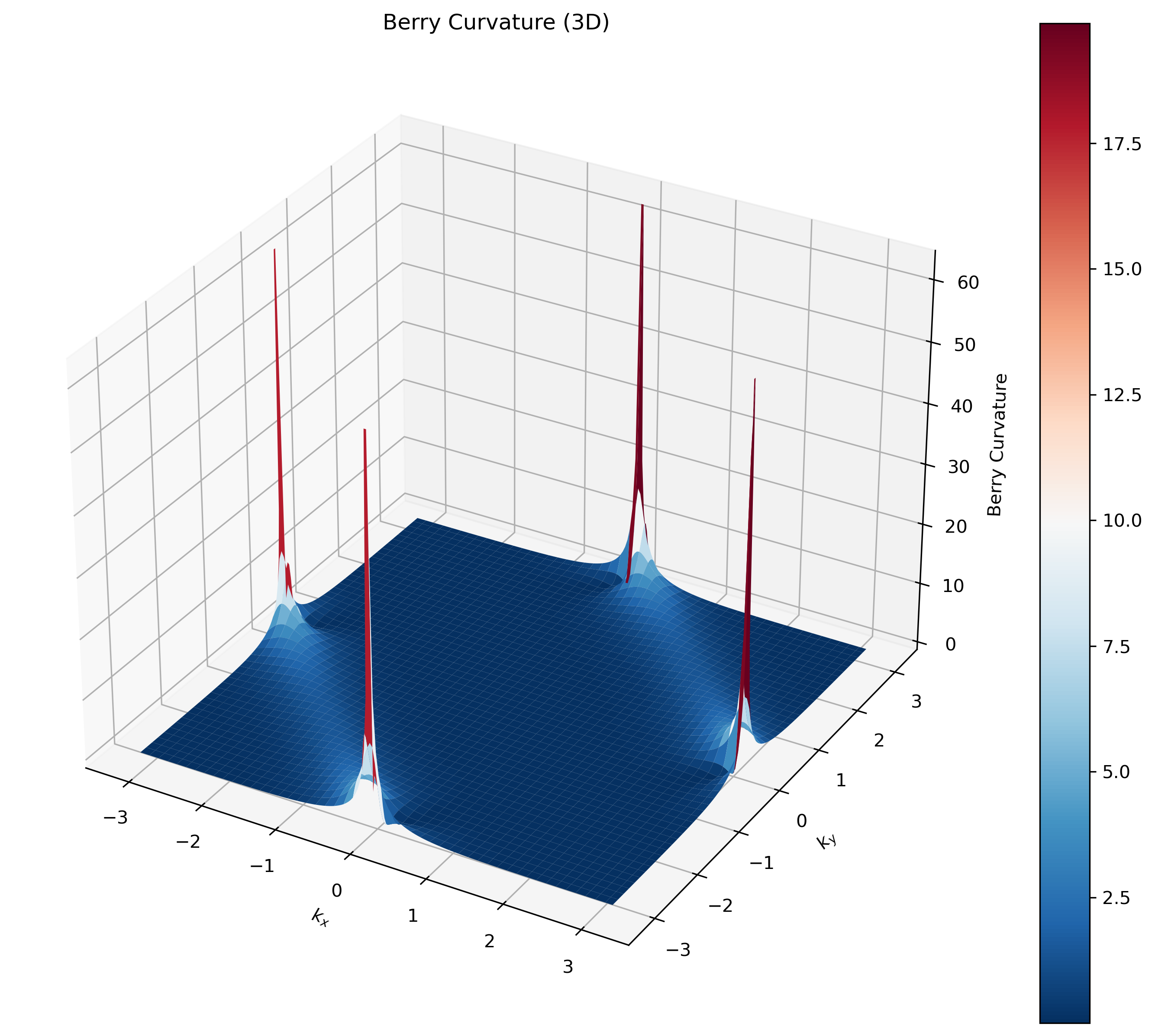
陈数是通过对整个布里渊区的Berry曲率积分得到的拓扑不变量:
$$C = \frac{1}{2\pi}\int_{\text{BZ}} F_{xy}(\mathbf{k})d^2\mathbf{k}$$
对于QWZ模型,当 $|u| < 2$ 时,陈数为 $C = \text{sgn}(u)$;当 $|u| > 2$ 时,陈数为 $C = 0$。这表明在 $|u| = 2$ 处系统发生拓扑相变。
数值模拟实现
在我们的Python实现中,我们使用了以下库:
- NumPy:用于数值计算
- Matplotlib:用于数据可视化
- Kwant:用于量子传输计算
代码实现了以下功能:
- 构建QWZ哈密顿量
- 计算能带结构
- 计算Berry曲率
- 计算陈数
- 可视化结果
高对称点的本征态
对于特殊的k点,如Γ点(0,0)、X点(π,0)和M点(π,π),我们计算了相应的本征态和本征值。这些点的本征态揭示了系统在动量空间中的重要量子特性。
结论
QWZ模型虽然简单,但它捕捉了拓扑绝缘体的本质特性。通过调整参数 $u$,系统可以经历拓扑相变,从拓扑平庸态转变为拓扑非平庸态,反之亦然。这种相变通过陈数的变化反映出来,并在Berry曲率的分布中清晰可见。
拓扑绝缘体的研究不仅具有理论意义,还有潜在的应用价值,例如在量子计算、自旋电子学和容错量子器件中的应用。
